
PHYSICS - Hangers Continue
OPENING QUESTION:
Consider the following examples of hanger problems.
Let's say you had to find the value of the tension forces for each rope in each case.
Contrast the following situations - how will your solution strategies differ? (Please Do NOT solve the problems, just discuss your strategies)
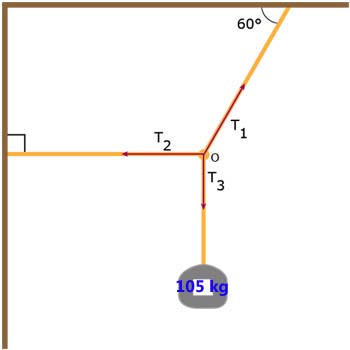
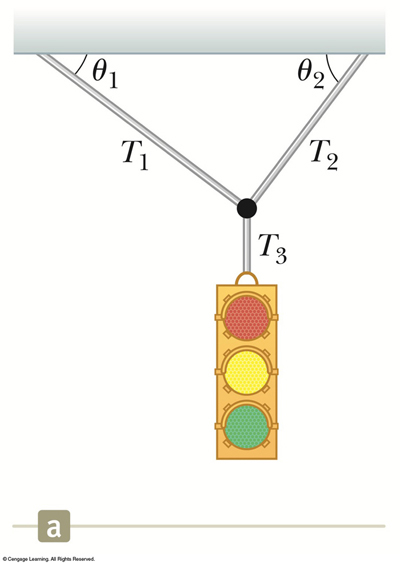
| The angle is 60.0 degrees (3 s.f.) the mass of the object is 105 kg as indicated. | Angle 1 is 37.0 degrees and angle 2 is 53.0 degrees. The mass of the stoplight is 75.0 kg. |
 |
 |
CALENDAR:
WORDS O' THE DAY:
-
Force ("Push" or "Pull")
-
Newton (kgm/s2)
-
Force Diagram (A sketch showing ALL forces acting on an object)
-
Net Force Diagram (A sketch showing only the resulting (net) forces acting on an object)
-
Newton's 1st Law ("An object will continue whatever it is currently doing unless acted on by an unbalanced force"
-
Newton's 3rd Law
-
-
(Short Version: "Forces ALWAYS come in pairs")
-
(Quick memory aid version: Noun1 Verb Noun2 | Noun2 Verb Noun1)
- (Formal Version: For every force acting on one object, there is an equal and opposite force acting on a second object
-
FORMULAE OBJECTUS:
- F = ma (Newton's 2nd Law)
- ΣFx = max (Newton's 2nd Law applied to multiple forces acting on an object horizontally) Notice how that works so well with Newton's 1st:
- If the sum of the forces acting on an object are unbalanced in x, the object will accelerate in x.
- If the sum of the forces acting on an object in x are balanced the object will continue doing whatever it is currently doing.
- If the object is at rest then the sum-of-the-forces-in-x MUST be balanced!!!
- ΣFy = may (Newton's 2nd Law applied to multiple forces acting on an object vertically) Notice how that works so well with Newton's 1st:
- If the sum of the forces acting on an object are unbalanced in y, the object will accelerate in y.
- If the sum of the forces acting on an object in y are balanced the object will continue doing whatever it is currently doing.
- If the object is at rest then the sum-of-the-forces-in-y MUST be balanced!!!
WORK O' THE DAY
Oh and by the by, I haven't forgotten about the nasty problem I sent you home with yesterday!
Here's a gentle warm-up:
1) The following forces are acting on an object with mass of 98.5 kg:
F1 pulls to the left with 33 N of force
F2 also pulls to the left with 88 N of force
F3 pulls to the right with 101 N of force
F4 pulls up with a force of 99 N of force
F5 pulls down with a force of 201 N
Notice that this is a fairly abstract/generic problem so we don't worry about gravity or the ground or any such since nothing like that is mentioned.
Sketch a force diagram
- Now please write a sum-of-the-forces version of Newton's 2nd in x
- Now please write a sum-of-the-forces version of Newton's 2nd in y
Now sketch a NET force diagram
Now please calculate the magnitude of the resulting vector
Now please calculate the ANGLE that vector makes to the horizontal
═══════════════════════════
2) Now let's take a swing at the first situation from the opening question. (Once again let's make that 60.0 degrees to add another coupla siggy figgies)
What key words must we look for in the description of this situation? What do they allow us to do?
How much force does the weight of the mass exert downwards?
Notice that the rope T1 is pulling upwards at an angle of 60.0 degrees. Further, notice that rope T2 is supporting no vertical forces whatsoever. That means that we must find the vertical component of rope T1 and that MUST equal T3. Why?
Do that now
Notice that the horizontal component of force of T1 MUST equal T2 (why?)
Calculate those now.
My written solution is HERE
Here's a solution to a tough one: Let's take a gander!
3) A stoplight is suspended by cables as shown below and is at rest:
3a) Junior Varsity Standard Version (This is a tough but a wee more gentle than b & c below):
Consider the stoplight with mass of 75 kg hanging at rest as shown above. Angle 1 is 37.0 degrees and angle 2 is 53.0 degrees. The mass of the stoplight is 75.0 kg. Find the forces T1 and T3 if we know that T2 = 590 N
- Sketch a force diagram
- Use the Alternate Interior Angle theorem to find helpful angles
- Use the weight of the stoplight to find T3
- Show the component (horizontal & vertical) forces for T1 and T2
- Write an equation that shows the horizontal components = 0
- Use those to solve for T1
My written solution is HERE
3b) Varsity Version (This is a tough one):
Consider the stoplight with mass of 75 kg hanging at rest as shown above. Angle 1 is 37 degrees and angle 2 is 53 degrees.
Find the forces T1 , T2 , T3 (pretend you DON'T know T2 )
- Sketch a force diagram
- Use the weight of the stoplight to find T3
- Show the component (horizontal & vertical) forces for T1 and T2
- Write an equation that shows the horizontal components = 0
- Use those to solve for T1 in terms of T2 (Note: this won't be an answer quite yet. It's just like algebra where you have two equations with two unknowns and you're trying to solve one of the unknowns. Remember that?)
- Write an equation that shows the vertical components = 0
- Substitute the value you found for T1 in terms of T2 above. Substitute your value for T3 above so now you have one equation with one unknown (*whew*)
- How will you find T2
My written solution is HERE & HERE
3c) Varsity Version (This is *tough*)
Now let's take this up one last final notch.
Image the same situation - almost as 3b:
Consider the stoplight with mass of 75 kg hanging at rest as shown above. Angle 1 is 37.0 degrees and angle 2 is 53.0 degrees. The mass of the stoplight is 75.0 kg. Find the forces T1 and T2 & T3
*gulp*
When I was a student I kept wanting/needing/pleading with my instructors to NOT give me problems without numbers... it seemed really weird to do problems in the abstract.
What I didn't know was how important to my learning of physics it was to process a problem and THEN worry about the numbers.
Towards that end I'm going to have you do just a wee bit of processing practice now. Remember, I will ALWAYS ask you to work a difficult problem for as long as you can work productively. This is another example of the Goldilocks Principle: Don't work too long on this problem, don't give up too soon.
Do a Newton's 1st analysis of the situation (Hint: the object is at rest, that means the stoplight isn't accelerating which means the forces acting on it MUST be balanced. That means the horizontal forces must be balanced AND the vertical forces acting on the stoplight MUST be balanced to
- Derive an equation for each of the component (vertical and horizontal) forces for T1 and T2 (hint: Dig back into the dim dark days of geometry and recall the alternate interior angle formula!)
Hint #1 is HERE
Hint #2 is HERE
Last Hint is HERE
3d) ADVANCED Varsity ++ Version (This is *tough*)
Now let's take this up one last final notch.
Image the same situation - almost as 3b:
Consider the stoplight with mass of 75 kg as shown above. Angle 1 is 67.0 degrees and angle 2 is 43.0 degrees. The mass of the stoplight is once 75.0 kg.
Find the resulting motion (if any) the object experiences.
We do NOT know if that object will remain at rest or not
*gulp*
When I was a student I kept wanting/needing/pleading with my instructors to NOT give me problems without numbers... it seemed really weird to do problems in the abstract (and by that I mean without numbers).
What I didn't know was how important to my learning of physics it was to process a problem and THEN worry about the numbers.
Towards that end I'm going to have you do just a wee bit of processing practice now. Remember, I will ALWAYS ask you to work a difficult problem for as long as you can work productively. This is another example of the Goldilocks Principle: Don't work too long on this problem, don't give up too soon.
Do a Newton's 1st analysis of the situation -- the object may or may not be at rest
Derive an equation for each of the component (vertical and horizontal) forces for T1 and T2 (hint: Dig back into the dim dark days of geometry and recall the alternate interior angle formula!)
Final Hint: Do your x-component and x-component on separate halves of your paper and ANNOTATE YOUR WORK
WOW